Reinforcement Learning In A Simple Card Game
In this document I will implement some model free reinforcement learning techniques to determine a policy for playing the card game tuppence ha’penny. This is based on techniques taught in the Sutton and Barto book and the UCL course on Reinforcement Learning 2015 by David Silver. The lectures are available on YouTube. The environment is my own creation based on a game which I play every Christmas with my in-laws. Each year I put 5 pence of my own money at stake so any improvement in my policy which I can gain by studying the problem would be quite beneficial.
The game has the following rules:
- Up to 5 cards are dealt to each player (less if there are more than 10 players)
- The deck of cards is a normal deck i.e. 13 values of 4 suits (the suits are not important to the game and neither are absolute values, the only important thing is that there are 13 different “types” of card and 4 of each “type”)
- Play progresses around the circle with each player laying 1 card
- If a player’s card matches the type (i.e. value) of the previous played card then the previous player loses a number of pence equal to 1 less than the number of cards in a row that have the same type
- e.g. if the sequence of card types played is 1 8 3 3 3 3 8 8, then the costs per player would be 0 0 1 2 3 0 1 0
- When a player runs out of money they are out of the game
- Once all cards have been played, cards are redealt to the remaining players until there is only 1 player left. This player then wins all of the money.
To reduce the number of states and simplify the learning process whilst still capturing the essence of the game, I will make the following simplifications:
- Players never run out of money
- There are always 10 players
- The player we control always has his turn last
The rewards are then simply the negative amount of money lost by our player. Note, that this doesn’t fully capture the advantage to making other players lose money. Future extensions to this work could remove some of these assumptions. However, hopefully this will reveal some useful tactics.
Implementation of Tuppence Ha’penny
The first task is to implement the Tuppence Ha’penny environment. First we import everything we need.
import random
import numpy as np
import matplotlib.pyplot as plt
import copy
import operator
from abc import ABC, abstractmethod
%matplotlib inline
Now we need a function to deal out the cards at the beginning of each episode.
def deal_cards(num_players=10):
"""
Deal 5 cards per player for up to 10 players, we only consider values we
don't preserve suits
"""
assert num_players <= 10
deck = list(range(13))*4
np.random.shuffle(deck)
hands = np.resize(deck, (num_players, 5))
return hands
The total relevant state of the system is somewhat complicated to work out. A simple, but wasteful representation would be to keep the number of cards of each type that the player has and to keep the entire sequence of played cards. The problem with this is that it makes the state space very large. We can easily see that many situations in this representation are equivalent. For example if I hold 4 aces and a 2 then it makes no difference to me if the player before me plays a 3 or a 4. Also, if I hold 3 2s and 2 4s, then this is entirely equivalent to holding 3 6s and 2 3s, i.e. the absolute values of the cards do not matter, just the number which are accounted for.
With this in mind we consider the relevant state to be:
- The number of cards of each type that the agent has
- The number of cards of each type that have been played (for the cards that the agent has)
- The type of the last card played
- The number of cards with the same type to have been played in a row before the agent’s turn
- The type of the last card played by the player ahead of the agent
The reason we care about the last card played by the player ahead is that it may tell us something about the remaining cards in their hand. For example if they started by playing a 3 it may be more likely that they have another 3 since to minimise their chance of the player ahead of them catching them out they may choose to play cards that they hold multiple of in their hand. You could argue that the entire played card history of the player ahead is relevant, and that if it is advantageous to catch out the player behind then their entire played hand is relevant too, but for simplicity we only consider the last card played by each.
To avoid duplicate states we transform the state so that:
- The agent’s cards have the lowest types
- Types are ordered by the number held by the agent (i.e. types which the agent holds more of are lower than types which the agent holds fewer of)
- If the agent holds the same number of multiple types then types are ordered by the number played (i.e. types of which there have been more played have lower types than those of which there have been fewer played)
- If the agent holds the same number of multiple types and both have been played the same number of times then if one was the last card played it will have a lower type than the other
- If the agent holds the same number of two types and both have been played the same number of times and neither was the last card played then if one was the last card played by the player ahead then it will have a lower type than the other
For example, if the player holds [6 6 9 12 1] and the following cards have been played previously [9 5 11 11 11 1 5 3 12] then we would transform 6 -> 0 since the player has 2 6s and only 1 of everything else, all of the remaining cards in the player’s hand have been played once so this rule has no effect, 12 -> 1 since it was the last card played, 9 -> 2 since it was the last card played by the player ahead, 1 -> 3 since it is held by the agent and must be lower than all cards not held by the agent but higher than all of the other cards held by the agent which have special properties, and the rest arbitrarily to fill the other numbers. Whereas if 1 had been played twice the transformation would be 6 -> 0, 1 -> 1, 12 -> 2, 9 -> 3, i.e. the 1 would take a lower type than the 12 and the 9 since it has been played twice whilst the 12 and 9 have only been played once each.
For each state we must consider what actions are available for the agent to take. The simplest answer to this question is that the agent can play any card in its hand. However, if there is only 1 possible action then there is no choice to make so we might as well not consider the state. Furthermore, if the agent has 2 different types in it’s hand and the agent holds the same number of them, the same number of them have been played and neither is the last card played or played by the player ahead then there is nothing in the state to distinguish between them and therefore we cannot learn that one is better than the other. Therefore, we may aswell only consider one of them.
We define a type to hold a single relevant state.
class State:
"""
Holds all the relevant state the agent knows about:
- player_1_counts: counts for each card type held
- played_counts: number played for each card type held
- last_card: the type of the last card played if held by the player or -1
otherwise
- num_played: the number of times in a row that the last card was played
before now
- played_by_player_ahead: the last card played by the player ahead
"""
def __init__(self, player_1_counts, played_counts, last_card, num_played,
played_by_player_ahead):
"""Set the state to copies of those passed in"""
self.player_1_counts = copy.deepcopy(player_1_counts)
assert np.all(player_1_counts[:-1] >= player_1_counts[1:])
self.played_counts = copy.deepcopy(played_counts)
self.last_card = copy.deepcopy(last_card)
self.num_played = copy.deepcopy(num_played)
self.played_by_player_ahead = copy.deepcopy(played_by_player_ahead)
def get_state_vector(self):
"""
Create a single vector to represent the state by concatenating all
variables
"""
return np.concatenate((self.player_1_counts, self.played_counts,
[self.last_card, self.num_played,
self.played_by_player_ahead]))
def __hash__(self):
"""Hash the state using all variables"""
return hash(tuple(self.get_state_vector().tolist()))
def __eq__(self, other):
"""Return if this state is equal to the one passed"""
return tuple(self.get_state_vector().tolist()) == \
tuple(other.get_state_vector().tolist())
def __ne__(self, other):
"""Return if this state is not equal to the one passed"""
return not(self == other)
def __str__(self):
"""Return a representation of this state as a string"""
return 'player_1_counts: ' + str(self.player_1_counts) + \
', played_counts: ' + str(self.played_counts) + \
', last_card: ' + str(self.last_card) + \
', num_played: ' + str(self.num_played) + \
', played_by_player_ahead: ' + str(self.played_by_player_ahead)
def calculate_actions_for_state(s):
"""
Return the set of actions which are distinct according to the state. Each
action is a card player 1 has.
"""
card_is_last_card = np.arange(len(s.player_1_counts)) == s.last_card
card_is_player_ahead_card = np.arange(len(s.player_1_counts)) == \
s.played_by_player_ahead
attributes = np.concatenate((s.player_1_counts.reshape(-1, 1),
s.played_counts.reshape(-1, 1),
card_is_last_card.reshape(-1, 1),
card_is_player_ahead_card.reshape(-1, 1)),
axis=1).T
unique_attributes, unique_actions = np.unique(attributes, axis=1,
return_index=True)
return unique_actions
def calculate_actions_for_state_vector(state_vector):
"""
Return the set of actions which are distinct according to the state. Each
action is a card player 1 has.
"""
s = State(state_vector)
return calculate_actions_for_state(s)
Below, we create a state-action space and functions to fill it with all the possible states considering that only states conforming to the transformation rules above will be possible.
class StateActionSpace:
"""
A class containing the states action space in the following variables:
- state_action_pairs: a dictionary of states to a dictionary of actions
- next_index: the number of state action pairs
"""
def __init__(self):
"""Initialise an empty state action space"""
self.next_index = 0
self.state_action_pairs = dict()
def add_state_action_pairs_to_state_action_space(state_action_space, state):
"""
Get all possible actions for the state and add them to the state action
space
"""
actions = calculate_actions_for_state(state)
if len(actions) > 1:
action_index_dict = dict()
for a in actions:
action_index_dict[a] = state_action_space.next_index
state_action_space.next_index += 1
state_action_space.state_action_pairs[state] = action_index_dict
return state_action_space
def consider_played_by_player_ahead(state_action_space, player_1_counts,
played_counts, last_card, num_played):
"""
Given the player 1 hand histogram and the number of cards of each type
played and the last card and the number of times in a row that it has been
played, consider what card could have been played by the player ahead. Then
get all possible actions for the state and add them to the state action
space.
"""
# Total cards played is 9 if I have a full hand of 5 cards, 19 if I have 4
# etc.
total_cards_played = (6 - np.sum(player_1_counts))*10 - 1
# The irrelevant cards are those we don't store in played_counts
num_irrelevant_cards_played = total_cards_played - np.sum(played_counts)
# If the last card was irrelevant then at least 1 irrelevant card is
# accounted for
if last_card == -1:
num_irrelevant_cards_played -= 1
# If we have at least 1 irrelevant card we can consider the state where the
# card played by the player ahead is irrelevant
if num_irrelevant_cards_played > 0:
s = State(player_1_counts, played_counts, last_card, num_played, -1)
state_action_space = add_state_action_pairs_to_state_action_space(
state_action_space, s)
# For each card type the player has the card played by the player ahead
# could take this value if they were not all the last cards played
played_unaccounted = copy.deepcopy(played_counts)
if last_card != -1:
played_unaccounted[last_card] -= num_played
for ahead in range(len(played_counts)):
if played_unaccounted[ahead] > 0:
s = State(player_1_counts, played_counts, last_card, num_played,
ahead)
state_action_space = add_state_action_pairs_to_state_action_space(
state_action_space, s)
return state_action_space
def consider_last_card(state_action_space, played_counts, player_1_counts):
"""
Given the player 1 hand histogram and the number of cards of each type
played consider what the last card played could have been and how many
times in a row it could have been played. Then consider the the remaining
part of the state - the last card played by the player ahead.
"""
# One possibility is that the last card played is irrelevant
total_cards_played = (6 - np.sum(player_1_counts))*10 - 1
num_irrelevant_cards_played = total_cards_played - np.sum(played_counts)
if num_irrelevant_cards_played > 0:
state_action_space = consider_played_by_player_ahead(
state_action_space, player_1_counts, played_counts, -1, 0)
# For each value played it could have been the last card and we could have
# had up to the number played in a row ending with the last card played
for p in range(len(played_counts)):
for n in range(played_counts[p]):
state_action_space = consider_played_by_player_ahead(
state_action_space, player_1_counts, played_counts, p, n + 1)
return state_action_space
def add_states_for_card_type(player_1_counts, j, min_j, state_action_space,
played_counts):
"""
Given the player 1 hand histogram, consider the card type j and consider
how many cards of this type could have been played already then recursively
call for the next card type j + 1. When all card types in the player's hand
have been considered, then consider the other parts of the state, last card
and played by player ahead.
"""
num_cards_in_hand = sum(player_1_counts)
# We are considering cards with value j
num_elsewhere = 4 - player_1_counts[j]
# Each card with value j which player 1 does not hold could have been
# played or not
for i in range(1+min([min_j, num_elsewhere])):
# Consider the possibilities if i j-value cards have been played
current_played_counts = copy.deepcopy(played_counts)
current_played_counts[j] = i
# If the j-value we are considering is the last distinct value held by
# player 1 then add all distinct possibilities calculated
if j == len(player_1_counts) - 1:
state_action_space = consider_last_card(state_action_space,
current_played_counts,
player_1_counts)
else:
# If we have more distinct values consider how many of them have
# been played
if player_1_counts[j] == player_1_counts[j+1]:
state_action_space = add_states_for_card_type(
player_1_counts, j + 1, i, state_action_space,
current_played_counts)
else:
state_action_space = add_states_for_card_type(
player_1_counts, j + 1, 1e9, state_action_space,
current_played_counts)
# We assume we are the last player in the circle so only consider
# possibilities where the correct number of cards have been played
if sum(current_played_counts) == ((6 - num_cards_in_hand)*10 - 1):
break
return state_action_space
def create_state_action_space():
"""
Create the set of all states we care about and the actions we can take in
them. Do not consider states with only one action since there is no
decision to make.
"""
# -1 means not applicable
hands = np.array([[0, 0, 0, 0, 1], [0, 0, 0, 1, 1], [0, 0, 0, 1, 2],
[0, 0, 1, 1, 2], [0, 0, 1, 2, 3], [0, 1, 2, 3, 4],
[-1, 0, 0, 0, 1], [-1, 0, 0, 1, 1], [-1, 0, 0, 1, 2],
[-1, 0, 1, 2, 3], [-1, -1, 0, 0, 1], [-1, -1, 0, 1, 2],
[-1, -1, -1, 0, 1]])
state_action_space = StateActionSpace()
for i in range(hands.shape[0]):
player_1_hand = hands[i, :]
player_1_counts = np.bincount(player_1_hand[player_1_hand >= 0])
state_action_space = add_states_for_card_type(
player_1_counts, 0, 1e9, state_action_space,
np.zeros((len(player_1_counts),), dtype=np.int))
return state_action_space
We create a dictionary of all states to another dictionary mapping the valid actions in this state to a unique index. This is provided at module scope so can be used by anything defined here.
state_action_space = create_state_action_space()
print('number of states:', len(state_action_space.state_action_pairs))
print('number of state action pairs:', state_action_space.next_index)
number of states: 4931
number of state action pairs: 16257
def get_actions_for_state(s):
"""Return all available actions for the passed state"""
return state_action_space.state_action_pairs[s].keys()
We also create an environment state. This is different to the player’s state since it must keep track of the cards in all players’ hands so that we can determine what actions they will take. We also define a function which implements a simple strategy where we just play the last card which was played if possible or the card which we account for the most of. This will be the strategy used by all non-agent players.
def play_simple_strategy(my_hand, played, last_card, num_played,
played_by_player_ahead, randomise=True):
"""
Play a simple strategy which is:
if I have a card of the same type as the last one to be played then play it
otherwise add my card counts to the played card counts and play the type
for which most are accounted
"""
# If I have a card which is the same as the last card then play it
if last_card != -1 and my_hand[last_card] > 0:
return last_card
# Otherwise add the cards I hold to the cards played and choose whichever
# is the largest
total_accounted_for = played + my_hand
total_accounted_for[my_hand == 0] = 0
if not randomise:
return np.argmax(total_accounted_for)
acceptable_indices = np.where(total_accounted_for ==
total_accounted_for.max())[0]
return np.random.choice(acceptable_indices)
class EnvironmentState:
"""
Store the entire state of the environment necessary to generate the
individual states for all players.
This consists of:
- hands: the counts for each card type for each player
- played: the counts for each card type played
- last card per player: the last card played by each player
- num_played: the number of times in a row that the last card has been
played (this could be worked out from last card per player but is
stored for efficiency)
- reward: the reward for player 1 since it was last consumed
"""
def __init__(self, hands, played, last_card_per_player, next_player):
"""
Initialise the variables to those passed in, calculate num_played and
set reward to 0.
"""
hand_bin_counts = np.zeros((10, 13), dtype=np.int)
for i in range(10):
hand_bin_counts[i, :] = np.bincount(hands[i, :], minlength=13)
self.hands = hand_bin_counts
self.played = played
self.last_card_per_player = last_card_per_player
self.reward = 0
last_player = next_player - 1 % len(last_card_per_player)
self.num_played = 0
last_card = self.last_card_per_player[last_player]
if last_card != -1:
while True:
self.num_played += 1
last_player = last_player - 1 % len(last_card_per_player)
card = self.last_card_per_player[last_player]
if card != last_card:
break
def play_card(self, player, card):
"""
Change the state by having the player passed in play the card passed
in.
"""
self.hands[player, card] -= 1
self.played[card] += 1
if self.last_card_per_player[player-1] != card:
self.num_played = 0
self.num_played += 1
self.last_card_per_player[player] = card
def update(self):
"""
Update the environment by having all other players play a simple
strategy and then transforming the state so that equivalent
environments are described by the same state. If the player has only
one possible action then automatically take it and update the
environment again.
"""
# For each player after the agent play the simple strategy
for i in range(1, self.hands.shape[0]):
next_player = (i + 1) % self.hands.shape[0]
card = play_simple_strategy(self.hands[i, :], self.played,
self.last_card_per_player[i-1],
self.num_played,
self.last_card_per_player[next_player])
# If this is the player immediately after the agent increment reward
# by negative of num_played
if i == 1 and card == self.last_card_per_player[i-1]:
self.reward -= self.num_played
self.play_card(i, card)
self.transform_state()
s = self.get_state()
actions_dict = state_action_space.state_action_pairs.get(s)
if not actions_dict:
actions_for_player_1 = calculate_actions_for_state(s)
# If the player only has one option take it
if len(actions_for_player_1) == 1:
self.play_card(0, actions_for_player_1[0])
if self.is_terminal():
return
self.update()
def transform_state(self):
"""
Transform the state so that equivalent environments are described by
the same state. This is described in more detail in the prose above.
"""
# First translate all cards so that player 1 has cards between 0 and 4
# with repeated cards having lower numbers
player_1_counts = self.hands[0, :]
# Next for any cards where player 1 has the same number of them sort by
# the number that have been played
# Next if player 1 has the same number of them and the same number have
# been played put last card first
# Next if player 1 has the same number of them and the same number have
# been played and neither are last card put played by player ahead
# first
attributes = zip(
-player_1_counts, -self.played,
-np.bincount([self.last_card_per_player[-1]], minlength=13),
-np.bincount([self.last_card_per_player[1]], minlength=13))
all_attributes = [(i, j, k, l) for i, j, k, l in attributes]
new_to_old = sorted(range(len(all_attributes)),
key=all_attributes.__getitem__)
old_to_new = np.argsort(new_to_old)
hands_new = np.zeros((self.hands.shape[0], 13), dtype=np.int)
for i in range(self.hands.shape[0]):
hands_new[i, :] = self.hands[i, new_to_old]
played_new = self.played[new_to_old]
last_card_per_player_new = old_to_new[self.last_card_per_player]
last_card_per_player_new[self.last_card_per_player == -1] = -1
self.hands = hands_new
self.played = played_new
self.last_card_per_player = last_card_per_player_new
cards_played_and_in_hands = np.sum(self.hands, axis=0) + self.played
assert np.all(cards_played_and_in_hands <= 4)
assert np.sum(cards_played_and_in_hands) == 5 * self.hands.shape[0]
def get_state(self):
"""
Get the player state from the environment state. State must have been
transformed using transform_state.
"""
hand = self.hands[0,:]
player_1_counts = hand[hand > 0]
# Cards the player has are the lowest values
relevant_played = self.played[:len(player_1_counts)]
last_card = self.last_card_per_player[-1]
played_by_player_ahead = self.last_card_per_player[1]
# Card only relevant if the player holds the same type
if last_card < len(player_1_counts):
last_card_if_relevant = last_card
num_played_if_relevant = self.num_played
else:
last_card_if_relevant = -1
num_played_if_relevant = 0
if played_by_player_ahead < len(player_1_counts):
played_by_player_ahead_if_relevant = played_by_player_ahead
else:
played_by_player_ahead_if_relevant = -1
return State(player_1_counts, relevant_played, last_card_if_relevant,
num_played_if_relevant,
played_by_player_ahead_if_relevant)
def is_terminal(self):
"""Return whether the episode is finished."""
return np.all(self.hands == 0)
def get_reward(self):
"""
Consume and return the reward accumulated since the last time the
reward was consumed
"""
ret = self.reward
self.reward = 0
return ret
def __str__(self):
"""Return a representation of this state as a string"""
return 'hands: \n' + str(self.hands) + \
',\nplayed: ' + str(self.played) + \
',\nlast_card_per_player: ' + str(self.last_card_per_player) + \
',\nnum_played: ' + str(self.num_played) + \
',\nreward: ' + str(self.reward)
def select_start_state():
"""Get a starting environment state"""
hands = deal_cards()
s = EnvironmentState(hands, np.zeros((13,), dtype=np.int),
np.full((10,), -1, dtype=np.int), 1)
s.update()
s.reward = 0
return s
Let’s see how the environment updates in a few cases.
for _ in range(2):
s = select_start_state()
print('start s', s)
if not s.is_terminal():
s.play_card(0, 0)
s.update()
print('s after one update', s)
start s hands:
[[1 1 1 1 1 0 0 0 0 0 0 0 0]
[0 1 0 0 0 1 1 0 1 0 0 0 0]
[0 0 0 1 0 0 0 0 1 1 0 0 1]
[0 0 0 0 1 0 1 0 0 0 2 0 0]
[1 0 0 1 0 0 0 0 0 0 0 1 1]
[0 0 0 0 1 0 1 2 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 1 0 0 2]
[0 0 0 0 1 1 0 0 0 1 0 1 0]
[0 0 1 1 0 0 0 0 0 0 1 1 0]
[0 0 2 0 0 0 0 0 0 1 0 1 0]],
played: [2 2 0 0 0 2 1 1 1 0 0 0 0],
last_card_per_player: [-1 5 1 6 8 1 7 5 0 0],
num_played: 2,
reward: 0
s after one update hands:
[[1 1 1 1 0 0 0 0 0 0 0 0 0]
[1 0 0 0 0 0 0 1 0 1 0 0 0]
[0 0 1 0 0 0 0 0 0 0 1 0 1]
[0 0 0 1 0 0 0 0 1 1 0 0 0]
[0 0 1 0 0 0 0 0 0 0 0 1 1]
[0 0 0 1 0 0 1 0 0 1 0 0 0]
[0 0 0 0 0 0 0 0 0 0 1 0 2]
[0 0 0 1 0 0 0 0 0 0 1 1 0]
[0 1 1 0 0 0 0 0 0 0 0 1 0]
[0 1 0 0 0 0 0 0 0 0 1 1 0]],
played: [2 1 0 0 4 4 3 2 2 1 0 0 0],
last_card_per_player: [5 4 7 8 5 6 6 4 8 1],
num_played: 1,
reward: 0
start s hands:
[[1 1 1 1 1 0 0 0 0 0 0 0 0]
[0 0 1 0 1 0 0 0 1 0 1 0 0]
[1 0 0 0 0 0 1 0 0 0 1 1 0]
[0 0 0 1 0 1 0 0 0 0 1 0 1]
[0 0 0 1 0 0 0 2 0 0 0 0 1]
[1 1 0 0 0 0 0 0 0 0 0 2 0]
[0 1 1 0 0 0 0 0 0 0 0 1 1]
[0 0 0 0 1 0 0 0 1 2 0 0 0]
[0 1 1 1 0 0 0 1 0 0 0 0 0]
[0 0 0 0 1 0 0 0 0 1 1 0 1]],
played: [1 0 0 0 0 3 3 1 1 0 0 0 0],
last_card_per_player: [-1 7 8 6 6 0 5 5 6 5],
num_played: 1,
reward: 0
s after one update hands:
[[1 1 0 0 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 0 0 0 1]
[0 0 0 0 0 0 0 0 0 0 0 0 1]
[0 0 0 0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 0 0 0 1]
[0 1 0 0 0 0 0 0 0 0 0 0 0]
[1 0 0 0 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0 0 0 0]],
played: [2 0 4 4 4 4 4 4 4 3 3 2 1],
last_card_per_player: [ 2 2 8 0 0 7 2 10 2 12],
num_played: 1,
reward: -1
In the second case shown above, after the first action is taken are card count reduces to 2 instead of 4. This is because all of our cards were indistinguishable from each other, so the environment arbitrarily chooses an action to take for us and progresses another 2 rounds before presenting us with our first state in which we can make a meaningful choice.
Finding the best policy
Now we will use reinforcement learning to determine the best policy. One thing that we could do is to calculate the probability of transitioning from each state to the next state and then do planning on the known MDP. However, this gets very complicated. Furthermore, the transition probabilities depend on the actions taken by the other players. In this case we have set them all to implement the same simple policy, but in general we would like to allow for substituting this with other policies, for example using other learning agents for the other players.
An alternative which does not require calculating the transition probabilities is to use model free control. Here we will only consider value based agents, i.e. agents where the policy is based on choosing an action with a high estimated value. To do this we will run a number of episodes (i.e. sample trajectories through the MDP) and use the actual cumulative rewards to the end of each episode that we get to estimate the value of each state. We can do this in a number of different ways, but all of the ones we consider can be updated in the ways you see in the following function.
def run_episodes(agent, num_episodes=int(1e6), gamma=1):
"""
Run a number of episodes choosing epsilon greedy actions, use agent passed
to update the estimates of state action values
"""
reward_per_episode = np.zeros((num_episodes,))
for episode in range(num_episodes):
if episode % 1e5 == 0:
print(episode, " out of ", num_episodes)
# Get the start state for the episode
while True:
environment_state = select_start_state()
if not environment_state.is_terminal():
break
s = environment_state.get_state()
a = agent.choose_action(s)
episode_reward = 0
# Run the episode until the state becomes terminal
while not environment_state.is_terminal():
agent.visit_state_action(s, a)
environment_state.play_card(0, a)
environment_state.update()
s_prime = environment_state.get_state()
# If the state we moved to is not terminal choose the next action
# now so that we can update algorithms like SARSA which learn q
q_prime = 0
a_prime = -1
if not environment_state.is_terminal():
a_prime = agent.choose_action(s_prime)
q_prime = agent.get_value(s_prime, a_prime)
reward = environment_state.get_reward()
agent.one_step_update(s, a, reward, s_prime, q_prime, gamma)
# Increment the episode reward
episode_reward += reward
s = s_prime
a = a_prime
# Update episodic algorithms like Monte Carlo learning
agent.update_end_of_episode(gamma)
reward_per_episode[episode] = episode_reward
return reward_per_episode
Based on the function above we need an agent of the following form. The update_end_of_episode, one_step_update and visit_state_action functions are to help the agent to improve, whereas the choose_action and get_value functions are required for us to continue. In this base class we let the agent do nothing to improve as this will all be done in derived classes and we let it delegate to a policy and value function to choose an action and get the value of a state action pair.
class Agent:
"""
Base class agent which defers action choice to a policy passed in and
getting the value of a state action pair to a value function which is also
passed in
"""
def __init__(self, policy, value_function):
"""Initialise the passed policy and value function"""
self.policy = policy
self.value_function = value_function
def update_end_of_episode(self, gamma):
"""
Do nothing to update the agent as this will be overridden by specific
agents
"""
pass
def one_step_update(self, s, a, r, s_prime, q_prime, gamma):
"""
Do nothing to update the agent as this will be overridden by specific
agents
"""
pass
def visit_state_action(self, state, action):
"""
Do nothing to update the agent as this will be overridden by specific
agents
"""
pass
def choose_action(self, state):
"""Defer to the policy to choose an action for the given state"""
return self.policy.choose_action(state)
def get_value(self, state, action):
"""
Defer to the value function to get the value for the given state action
pair
"""
return self.value_function.get_value(state, action)
class Policy(ABC):
"""The interface for a policy is just a choose action function"""
@abstractmethod
def choose_action(self, state):
"""We do nothing here as this must be overridden"""
pass
We don’t have to use a learning agent in this scheme, we just need some way of choosing an action. To give a baseline performance let’s see how the agent performs using the same simple strategy that the other players use.
class SimpleStrategy(Policy):
"""
An agent which does not learn but uses a simple strategy of playing the
last card played if possible or else playing the card which we can account
for the most of
"""
def choose_action(self, state):
"""Just play a simple non-learned strategy to choose an action"""
return play_simple_strategy(state.player_1_counts,
state.played_counts,
state.last_card,
state.num_played,
state.played_by_player_ahead)
class EmptyValue:
"""Value function which always gives a value of 0"""
def get_value(self, state, action):
"""Return 0 regardless of input"""
return 0
def get_simple_agent():
"""Return a simple non-learning agent"""
return Agent(SimpleStrategy(), EmptyValue())
To see how this performs we ran it for 100,000 episodes. Unsurprisingly, the rewards per episode are very variable. To smooth them out we take a rolling mean of 10,000 episodes. We run this 100 times and take an average. I haven’t shown the training process here but it should be clear, we just create a simple agent, and pass it to the run episodes function, we do this 100 times saving the result of each. Below I read these results back in and display the smoothed average result.
reward_per_episode_100 = np.zeros((100, int(1e5)))
for i in range(100):
reward_per_episode_100[i, :] = np.load(
'reward_per_episode_simple' + str(i) + '.npy')
mean_reward_per_episode_simple = np.mean(reward_per_episode_100, axis=0)
plt.figure()
plt.plot(np.convolve(mean_reward_per_episode_simple, np.ones((10000,))/10000,
mode='valid'))
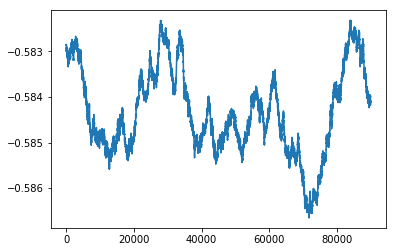
As expected, the results do not improve over the course of the run they stick around -0.584.
For the learning agents that we consider we will need some kind of value function that can estimate the value for a state action pair and update the value based on the error in its estimate and some value, $\alpha$, to scale the error.
class ValueFunction(ABC):
"""Base class for a value function"""
@abstractmethod
def get_value(self, state, action):
"""
The derived class should override this with a function returning an
estimate of the value of the passed state action pair
"""
pass
@abstractmethod
def update_value(self, state, action, error, alpha):
"""
The derived class may override this with a function updating the
estimate of the value of the passed state action pair (and any other
state action pairs it wishes to update)
"""
pass
@abstractmethod
def update_all_values(self, error, alpha):
"""
The derived class may override this with a function updating all
estimated values
"""
pass
def get_action_values(self, state):
"""Returns estimates for all available actions from this state"""
available_actions = get_actions_for_state(state)
return {a: self.get_value(state, a) for a in available_actions}
The simplest way to store these values is to have a table with one value for each state action pair and update the state action pairs that we visit.
class LookupTableValueFunction(ValueFunction):
"""
Value function which stores a value for all state action pairs in the
StateActionSpace passed in
"""
def __init__(self, state_action=state_action_space):
"""
Set the StateActionSpace passed in and initialise the value table to 0s
"""
self.state_action = state_action
self.value_table = np.zeros((self.state_action.next_index,))
def get_value(self, state, action):
"""Return the stored value for the state action pair passed in"""
return self.value_table[self.state_action.state_action_pairs[state][action]]
def update_value(self, state, action, error, alpha):
"""
Update the value for the state action pair passed in by incrementing by
alpha*error
"""
self.value_table[self.state_action.state_action_pairs[state][action]] \
+= alpha*error
def update_all_values(self, error, alpha):
"""Update all stored values by incrementing by alpha*error"""
self.value_table += alpha*error
def set_value_table(self, value_table):
"""Replace the stored value table with the one passed in"""
self.value_table = value_table
As for how to update the values, we are trying to estimate the cumulative reward that we will receive by the end of the episode given the state we are in. A simple way to estimate this is by recording the rewards we receive during the episode and then calculating the cumulative reward and updating the value for all visited states based on the cumulative reward at the end of each episode. This is known as Monte-Carlo learning.
class MonteCarloAgent(Agent):
"""
Learning agent which uses full episode returns to update estimated state
action values
"""
def __init__(self, policy, alpha_getter, value_function):
"""
Initialise the policy and value function by passing to the base class,
initialise a method for getting an alpha value where alpha is the
amount to move the value estimate in the direction of the latest
return.
Initialise an empty list, state_action_reward, to store the state
action pairs visited and the rewards received until the end of the
episode.
"""
super().__init__(policy, value_function)
self.alpha_getter = alpha_getter
self.state_action_reward = []
def one_step_update(self, s, a, r, s_prime, q_prime, gamma):
"""
Record the state action pair visited and the reward received and
generate an alpha value for it.
"""
self.state_action_reward.append(
[s, a, r, self.alpha_getter.alpha(s, a)])
def update_end_of_episode(self, gamma):
"""
Do the update at the end of the episode by calculating the cumulative
reward for each state visited and incorporating it in the value
estimate
"""
cumulative_reward = 0
for sara in reversed(self.state_action_reward):
s = sara[0]
a = sara[1]
cumulative_reward += sara[2]
sara[2] = cumulative_reward
for sara in self.state_action_reward:
s = sara[0]
a = sara[1]
current_value = self.value_function.get_value(s, a)
cumulative_reward = sara[2]
self.value_function.update_value(s, a,
cumulative_reward - current_value,
sara[3])
cumulative_reward *= gamma
self.state_action_reward = []
This leaves us with 2 things to determine:
- How much to scale the error by when updating the value estimates.
- How to set the policy based on the value function.
Both of these issues are explore in more detail in the post “Multi-Armed Bandits”. For the first issue, since this is a simple stationary problem we will use $\alpha = \frac{1}{N(s,a)}$ where $N(s,a)$ is the number of times we have visited the state action pair we are updating. This implements an incremental average calculation so gives the average return for each state action pair.
class IncrementalAverageAlpha:
"""
A method for getting an alpha value where alpha is the amount to move the
value estimate in the direction of the latest return. The alpha value given
is 1/(number of visits to state action pair). This ensures that the value
estimate is an average of the returns.
"""
def __init__(self, count_table_holder):
"""
Initialise a count table holder which holds a count of the number of
visits to each state action pair.
"""
self.count_table_holder = count_table_holder
def alpha(self, state, action):
"""
Return an alpha value of 1/(number of visits to state action pair) for
the state action pair passed in.
"""
count = self.count_table_holder.get_state_action_count(state, action)
alph = 1.0/count
return alph
def alpha_all_states(self):
"""
Return an alpha value of 1/(number of visits to state action pair) for
all state action pairs
"""
valid_states = np.where(self.count_table_holder.count_table > 0)
alph = np.zeros(self.count_table_holder.count_table.size)
counts = self.count_table_holder.count_table[valid_states[0]]
alph[valid_states[0]] = np.divide(1.0, counts)
return alph
For this we need to keep track of the number of times we have visited each state, which we will do using another simple table with one value per state action pair.
class CountTableHolder:
"""
A type which holds a table to count the number of visits to each state
action pair for the StateActionSpace passed in
"""
def __init__(self, state_action=state_action_space):
"""Initialise the count for all state action pairs to 0"""
self.state_action = state_action
self.count_table = np.zeros((self.state_action.next_index,))
def visit_state_action(self, state, action):
"""Increment the count for the state action pair passed in"""
self.count_table[self.state_action.state_action_pairs[state][action]] \
+= 1
def get_state_count(self, state):
"""Get the count for all state action pairs for the passed state"""
indices = self.state_action.state_action_pairs[state].values()
return [self.count_table[i] for i in indices]
def get_state_action_count(self, state, action):
"""Get the count for the passed state action pair"""
index = self.state_action.state_action_pairs[state][action]
return self.count_table[index]
For the second issue of how to choose an action based on the value estimates, the simplest thing is to compare the values for each available action and choose the one with the maximum value. This is known as a greedy policy.
class GreedyPolicy(Policy):
"""A policy which returns the action with the maximum value"""
def __init__(self, value_function):
"""Initialise the value function passed in"""
self.value_function = value_function
def choose_action(self, state):
"""Return the action with the maximum value"""
# The best action is the one with the greatest estimated value
action_values = self.value_function.get_action_values(state)
return max(action_values.items(), key=operator.itemgetter(1))[0]
The problem with this is that we can get stuck in some sub-optimal part of the state action space before we have a good estimate of the values in the rest of the state action space. We never explore the remainder of the state action space because our early estimates of the values are low. This is known as the exploration-exploitation problem and is explored more in “Multi-Armed Bandits”. One simple way to allow continued exploration is to choose a random action with some small probability $\varepsilon$, and otherwise to use a greedy policy.
class EpsilonGreedy(Policy, ABC):
"""
A policy which with probability epsilon returns a random action, otherwise
it returns the action with the maximum value
"""
def __init__(self, value_function):
"""Initialise a greedy policy using the value function passed in"""
self.greedy_policy = GreedyPolicy(value_function)
def choose_action(self, state):
"""
With probability epsilon returns a random action, otherwise it
returns the action with the maximum value
"""
action_prob = random.random()
# Choose randomly from the available actions with probability epsilon
# otherwise choose the best action
if action_prob < self.epsilon(state):
available_actions = \
list(state_action_space.state_action_pairs[state].keys())
i = random.randint(0, len(available_actions) - 1)
return available_actions[i]
return self.greedy_policy.choose_action(state)
@abstractmethod
def epsilon(self, state):
"""
Derived classed should override to return the probability of
returning a random action
"""
pass
The only remaining question is how to choose $\varepsilon$. Since we have a count for the times we have visited each state action pair we can make use of this to encourage more exploration early on by setting $\varepsilon = \frac{N_0}{N_0 + \sum_{a \epsilon A(s)}N(s,a)}$ for some constant $N_0$, where $A(s)$ is the set of available actions in state $s$. This means that for the first $N_0$ visits to this state action pair we will choose an action at random with a probability greater than half and it will gradually decrease as $N(s,a)$ increases.
class EpsilonDecayN0(EpsilonGreedy):
"""
An epsilon greedy policy which defines epsilon as n0/(n0 + num times state
visited) to encourage early exploration
"""
def __init__(self, n0, count_table_holder, value_function):
"""
Initialise the epsilon greedy base class with the value function passed
and store count table and n0 so we can calculate epsilon as n0/(n0 +
num times state visited)
"""
self.count_table_holder = count_table_holder
self.n0 = n0
super().__init__(value_function)
def epsilon(self, state):
"""Return n0/(n0 + num times state visited)"""
state_count = self.count_table_holder.get_state_count(state)
return self.n0/(self.n0 + np.sum(state_count))
Putting this all together into one agent we have the following:
class MCAverageEpsilonN0(MonteCarloAgent):
"""
This agent learns using Monte-Carlo estimates i.e. by calculating the
average cumulative reward to the end of the episode for each state visited.
It uses an epsilon greedy policy where epsilon decreases as the state is
visited more and an alpha value which calculates an incremental average of
the returns seen. The values for each state action pair are stored in a
lookup table.
"""
def __init__(self, n0=10):
"""
Initialise the base class with an epsilon greedy policy where epsilon
decreases as the state is visited more, an alpha value which calculates
an incremental average of the returns seen, and a lookup table value
function. Store a count table to facilitate these.
"""
self.count_table_holder = CountTableHolder()
value_function = LookupTableValueFunction()
super().__init__(EpsilonDecayN0(n0, self.count_table_holder,
value_function),
IncrementalAverageAlpha(self.count_table_holder),
value_function)
def visit_state_action(self, state, action):
"""Update the count table"""
self.count_table_holder.visit_state_action(state, action)
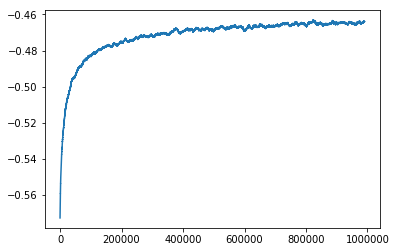
We can now see how this learning agent performs on the problem. We run the agent for 1,000,000 episodes to see how the performance improves as it learns. As with the simple strategy agent we do this 100 times and average the results and we take a rolling mean over 10,000 episodes.
reward_per_episode_100 = np.zeros((100, int(1e6)))
for i in range(100):
reward_per_episode_100[i, :] = np.load('reward_per_episode_aggregate' +
str(i) + '.txt.npy')
mean_reward_per_episode = np.mean(reward_per_episode_100, axis=0)
plt.figure()
plt.plot(np.convolve(mean_reward_per_episode, np.ones((10000,))/10000,
mode='valid'))
plt.figure()
plt.plot(np.convolve(mean_reward_per_episode[:100000], np.ones((10000,))/10000,
mode='valid'), label='Monte Carlo')
plt.plot(np.convolve(mean_reward_per_episode_simple, np.ones((10000,))/10000,
mode='valid'), label='Simple strategy')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
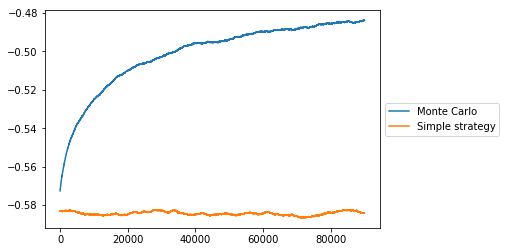
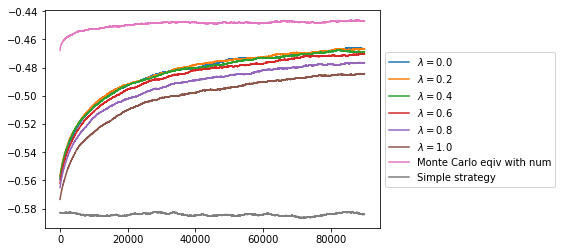
This makes a big improvement over the simple strategy agent and over the course of the 1,000,000 episodes the average reward per episode increases to -0.464. The only problem here is that 1,000,000 episodes takes a long time to run and it looks like the average reward per episode is still increasing.
Backward view Sarsa($\lambda$)
Part of the reason it is taking a long time to converge is that there is a lot of variance in what happens in the remaining part of the episode after we have selected an action in a state i.e. after the agent decides to play a card in the first round any number of things could happen and we need to average all of them together to get an accurate estimate for the value of this early state.
An alternative is to bootstrap by using single rewards seen in a state action pair and then using the current estimate of the value function for the state action pair we end up at. This is called TD(0) and gives a biased estimate with low variance as opposed to the unbiased Monte-Carlo method which has high variance. More generally we can trade off bias and variance by considering trajectories of different lengths up to $\infty$ and combining them in the following way:
This is known as TD($\lambda$).
Instead of waiting for episodes to finish before calculating this we can broadcast rewards backwards to earlier states by keeping track of how eligible each state will be for the current reward as we go. This calculates the exact same thing as if we had waited until the end of the episode.
class BackwardSarsaAgent(Agent):
"""
This agent learns using backward view Sarsa lambda estimates i.e. using one
step updates to update the value of all eligible states.
"""
def __init__(self, lambda_val, eligibility_trace, policy, alpha_getter,
value_function):
"""
Initialise the base class with the policy and value function passed.
Set the alpha getter, lambda val and eligibility trace for later use
"""
super().__init__(policy, value_function)
self.alpha_getter = alpha_getter
self.lambda_val = lambda_val
self.eligibility_trace = eligibility_trace
def one_step_update(self, s, a, r, s_prime, q_prime, gamma):
"""
Update the value at s, a based on the reward seen and our estimate of
the value at the subsequent state action pair. Also update all previous
states visited this episode which are still eligible. Update the
eligibility of states.
"""
delta = r + \
gamma*q_prime - \
self.value_function.get_value(s, a)
self.eligibility_trace.increment(s, a)
alpha = self.alpha_getter.alpha_all_states()
self.value_function.update_all_values(
delta,
np.multiply(alpha, self.eligibility_trace.eligibility_trace))
self.eligibility_trace.one_step_update(gamma, self.lambda_val)
def update_end_of_episode(self, gamma):
"""At the end of each episode reset the eligibility traces"""
self.eligibility_trace.update_end_of_episode()
We can use the same kind of policies, value functions and $\alpha$ values as before but we do need a new type to keep track of the eligibility trace per state.
class LookupEligibilityHolder:
"""
This type stores the eligibility of state action pairs to be updated when a
reward is seen.
"""
def __init__(self, state_action=state_action_space):
"""
Initialise an eligibility trace table to 0s with one element per state
action pair in the state action space passed
"""
self.state_action = state_action
self.eligibility_trace = np.zeros((self.state_action.next_index,))
def increment(self, state, action):
"""Increment the eligibility of the state action pair passed"""
index = self.state_action.state_action_pairs[state][action]
self.eligibility_trace[index] += 1
def one_step_update(self, gamma, lambda_val):
"""Update the state action pair by multiplying by gamma and lambda"""
self.eligibility_trace *= gamma*lambda_val
def update_end_of_episode(self):
"""At the end of each episode reset the eligibility to 0"""
self.eligibility_trace = np.zeros((self.state_action.next_index,))
We can then put it all together in the following agent.
class SarsaAverageEpsilonN0(BackwardSarsaAgent):
"""
This agent learns using sarsa. It uses an epsilon greedy policy where
epsilon decreases as the state is visited more and an alpha value which
calculates an incremental average of the returns seen. The values for each
state action pair are stored in a lookup table.
"""
def __init__(self, lambda_val, n0=10):
"""
Initialise the base class with an epsilon greedy policy where epsilon
decreases as the state is visited more, an alpha value which calculates
an incremental average of the returns seen, and a lookup table value
function. Store a count table to facilitate these.
"""
self.count_table_holder = CountTableHolder()
value_function = LookupTableValueFunction()
super().__init__(lambda_val,
LookupEligibilityHolder(),
EpsilonDecayN0(n0, self.count_table_holder,
value_function),
IncrementalAverageAlpha(self.count_table_holder),
value_function)
def visit_state_action(self, state, action):
"""Update the count table"""
self.count_table_holder.visit_state_action(state, action)
After trying this with various values of $\lambda$ we can see how it compares to Monte Carlo and to the simple strategy. As expected $\lambda = 1$ is equivalent to Monte Carlo. All of the other values for $\lambda$ improve the speed of convergence with the lowest values doing the best. This indicates that in this game the long term effect of actions is small compared to the short term effects, i.e. if we play a 3 in the last round of an episode and get a reward of -1 it was not made much more likely by the card we played in the first round, so broadcasting the change in reward back to the action chosen in the first round does not benefit us it just increases the variance.
plt.figure()
for j, lambda_val in enumerate(np.linspace(0.0, 1.0, 6)):
reward_per_episode_sarsa_100 = np.zeros((100, int(1e5)))
for i in range(100):
reward_per_episode_sarsa_100[i, :] = np.load(
'reward_per_episode_bsa' + str(i) + '_' + str(lambda_val) + '.npy')
mean_reward_sarsa = np.mean(reward_per_episode_sarsa_100, axis=0)
plt.plot(np.convolve(mean_reward_sarsa, np.ones((10000,))/10000,
mode='valid'),
label='$\lambda = ' + str(lambda_val) + '$')
plt.plot(np.convolve(mean_reward_per_episode[:100000], np.ones((10000,))/10000,
mode='valid'), label='Monte Carlo')
plt.plot(np.convolve(mean_reward_per_episode_simple, np.ones((10000,))/10000,
mode='valid'), label='Simple strategy')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
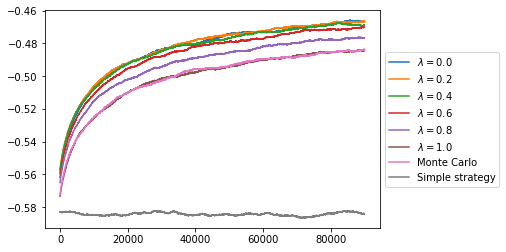
Function Approximation
Another way that we can speed up convergence is to share learning across similar states by learning a function which approximates the value of each state action pair instead of storing it directly. For example, if we learn that it is good to play a 0 when we hold 2 of them and a 1 and a 2, then it may be beneficial to also update the value of playing a 0 when we hold 2 of them and 2 1s. There are many ways to approximate the value function, the most common are neural networks and linear combinations of features.
If we assume that the function approximator, $\hat{v}$, is differentiable we can define a cost function as the mean squared error between the approximator and the actual returns, $G_t$, or TD($\lambda$) target, $G_t^{\lambda}$, and use gradient descent to update the approximator’s parameters.
With a linear combination of features:
So we could implement this by replacing the value function with the following for some get_features function which extracts features for any state action pair.
class LinearCombinationValueFunction(ValueFunction):
"""
Value function which stores a value for each feature which can be extracted
from a state action pair
"""
def __init__(self, get_features, num_features):
"""
Initialise a function to get features from a state action pair and
initialise a value table to 0s for each of the features.
"""
self.get_features = get_features
self.value_table = np.zeros((num_features,))
def get_value(self, state, action):
"""
Get the features for the state action pair passed in and calculate the
value based on these.
"""
f = self.get_features(state, action)
return np.dot(self.value_table, f)
def update_value(self, state, action, error, alpha):
"""
Update the values of all features which are non zero for this state
action pair
"""
f = self.get_features(state, action)
self.value_table += alpha*error*f
def update_all_values(self, error, alpha):
"""Update the values of all features"""
self.value_table += alpha*error
def set_value_table(self, value_table):
"""Set the value table to the one passed in"""
self.value_table = value_table
In fact, even the lookup table can be considered a special case of a linear combination of features where each feature is set to 1 if we are in the state action pair that it corresponds to.
I have experimented with various features to extract from the state action space. The most successful of which is another form of linear combinations of features. In this approach we set the values of different state action pairs to be the same. This is effectively like reducing the state space. For this form of function approximation we can use a simplified value function.
class LookupEquivalentStates(LookupTableValueFunction):
"""
Value function which converts one state action type to another and stores
one value for each of the converted state action type
"""
def __init__(self, state_action_converter, state_action_space):
"""
Initialise the state action converter and pass the state action space
to the base class to allow it to create a value table for each of the
converted state action pairs
"""
self.state_action_converter = state_action_converter
super().__init__(state_action_space)
def get_value(self, state, action):
"""
Return a value for the state action pair passed by converting to
another state action type and looking up the value stored for that
"""
return super().get_value(self.state_action_converter(state, action), 0)
def update_value(self, state, action, error, alpha):
"""
Update the value of the state action pair by converting to another
state action type and updating the value stored for that
"""
return super().update_value(self.state_action_converter(state, action),
0, error, alpha)
For example, perhaps we can perform well if for each state action pair we only consider parts of the state which relate to the action we are estimating the value for. We can represent this information with the state below.
class SingleCardNumState:
"""
Type which holds the number of cards of a specific type held by an agent,
the number of that type of card already played, whether the last card was
of that type, the number of cards of that type played in a row immediately
before the agents turn, whether the card played by the player ahead is of
that type, and the total number of cards of all types held by the player
"""
def __init__(self, held, played, last_card, num_played,
played_by_player_ahead, num_cards):
"""
Set the number of cards of a specific type held by an agent, the number
of that type of card already played, whether the last card was of that
type, the number of cards of that type played in a row immediately
before the agents turn, whether the card played by the player ahead is
of that type, and the total number of cards of all types held by the
player
"""
self.held = held
self.played = played
self.last_card = last_card
self.num_played = num_played
self.played_by_player_ahead = played_by_player_ahead
self.num_cards = num_cards
def get_state_vector(self):
"""
Create a single vector to represent the state by concatenating all
variables
"""
return np.array([self.held, self.played, self.last_card,
self.num_played, self.played_by_player_ahead,
self.num_cards])
def __hash__(self):
"""Hash the state using all variables"""
return hash(tuple(self.get_state_vector().tolist()))
def __eq__(self, other):
"""Return if this state is equal to the one passed"""
return tuple(self.get_state_vector().tolist()) == \
tuple(other.get_state_vector().tolist())
def __ne__(self, other):
"""Return if this state is not equal to the one passed"""
return not(self == other)
def __str__(self):
"""Return a representation of this state as a string"""
return 'held: ' + str(self.held) + \
',\nplayed: ' + str(self.played) + \
',\nlast_card: ' + str(self.last_card) + \
',\nnum_played: ' + str(self.num_played) + \
',\nplayed_by_player_ahead: ' + \
str(self.played_by_player_ahead) + \
',\nnum_cards: ' + str(self.num_cards)
For our value function we need to be able to convert state action pairs from the original type to the new type and then have a state action space where we can look up the index into the reduced value table.
def consider_cards_equivalent_num(state, action):
"""
Function which converts the state action pair passed in to a
SingleCardNumState just considering the card of the type of action we are
evaluating
"""
last_card = -1
num_played = 0
if action == state.last_card:
last_card = 0
num_played = state.num_played
return SingleCardNumState(state.player_1_counts[action],
state.played_counts[action],
last_card, num_played,
0 if action == state.played_by_player_ahead
else -1,
np.sum(state.player_1_counts))
single_card_num_states = set()
for state, actions_dict in state_action_space.state_action_pairs.items():
for action in actions_dict.keys():
converted = consider_cards_equivalent_num(state, action)
single_card_num_states.add(converted)
equivalent_action_num_state_space = StateActionSpace()
equivalent_action_num_state_space.state_action_pairs = \
{s : {0 : i} for i, s in enumerate(single_card_num_states)}
equivalent_action_num_state_space.next_index = \
len(equivalent_action_num_state_space.state_action_pairs)
We can also store a count table the size of our reduced state action space to accurately reflect the number of samples we have for each new state so that we can decay $\varepsilon$ and set $\alpha$ correctly.
class CountTableHolderEquivalentStates(CountTableHolder):
"""
Type which converts state action pairs to SingleCardNumStates before
counting the visits to each SingleCardNumState
"""
def __init__(self, state_action_converter, state_action_space):
"""
Initialise the state action converter and pass the state action space
to the base class so that it can initialise a count table for each
state action pair
"""
self.state_action_converter = state_action_converter
self.state_action_space = state_action_space
super().__init__(self.state_action_space)
def visit_state_action(self, state, action):
"""
Base class increments the count for the state action pair converted
to a SingleCardNumStates
"""
super().visit_state_action(self.state_action_converter(state, action),
0)
def get_state_count(self, state):
"""Get the count for all available actions in the passed state"""
converted_states = [self.state_action_converter(state, a)
for a in get_actions_for_state(state)]
indices = [self.state_action_space.state_action_pairs[s][0]
for s in converted_states]
return [self.count_table[i] for i in indices]
def get_state_action_count(self, state, action):
"""
Base class returns the count for the state action pair converted to a
SingleCardNumStates
"""
return super().get_state_action_count(
self.state_action_converter(state, action), 0)
Putting it all together we have the following agent.
class MCAverageEpsilonN0EquivNum(MonteCarloAgent):
"""
This agent learns using Monte-Carlo estimates i.e. by calculating the
average cumulative reward to the end of the episode for each
SingleCardNumState which can be converted to from a state action pair
visited. It uses an epsilon greedy policy where epsilon decreases as the
SingleCardNumState is visited more and an alpha value which calculates an
incremental average of the returns seen. The values for each
SingleCardNumState are stored in a lookup table.
"""
def __init__(self, n0=10):
"""
Initialise the base class with an epsilon greedy policy where epsilon
decreases as the SingleCardNumState is visited more, an alpha value
which calculates an incremental average of the returns seen, and a
lookup table value function which converts from a state action pair to
a SingleCardNumState. Store a count table which does the same
conversion to facilitate these.
"""
self.count_table_holder = CountTableHolderEquivalentStates(
consider_cards_equivalent_num, equivalent_action_num_state_space)
value_function = LookupEquivalentStates(
consider_cards_equivalent_num, equivalent_action_num_state_space)
super().__init__(EpsilonDecayN0(n0, self.count_table_holder,
value_function),
IncrementalAverageAlpha(self.count_table_holder),
value_function)
def visit_state_action(self, state, action):
"""Update the count table"""
self.count_table_holder.visit_state_action(state, action)
Comparing the results to our previous strategies this has very quickly reached a value higher than we have been able to achieve with any other strategy. This is because we get far more examples of each state action pair in the reduced space, and clearly the new state action space does not lose much information compared with the full state action space.
reward_per_episode_100 = np.zeros((100, int(1e5)))
for i in range(100):
reward_per_episode_100[i, :] = np.load('reward_per_episode_equiv_num' +
str(i) + '.npy')
mean_reward_per_episode_equiv_num = np.mean(reward_per_episode_100, axis=0)
plt.figure()
for j, lambda_val in enumerate(np.linspace(0.0, 1.0, 6)):
reward_per_episode_sarsa_100 = np.zeros((100, int(1e5)))
for i in range(100):
reward_per_episode_sarsa_100[i, :] = np.load(
'reward_per_episode_bsa' + str(i) + '_' + str(lambda_val) + '.npy')
mean_reward_sarsa = np.mean(reward_per_episode_sarsa_100, axis=0)
plt.plot(np.convolve(mean_reward_sarsa, np.ones((10000,))/10000,
mode='valid'),
label='$\lambda = ' + str(lambda_val) + '$')
plt.plot(np.convolve(mean_reward_per_episode_equiv_num[:100000],
np.ones((10000,))/10000, mode='valid'),
label='Monte Carlo eqiv with num')
plt.plot(np.convolve(mean_reward_per_episode_simple[:100000],
np.ones((10000,))/10000, mode='valid'),
label='Simple strategy')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
Tactics Learned
Using reinforcement learning techniques we have found a policy which improves the average reward per episode from around -0.58 using a simple strategy to more than -0.45. So what have we learned about how to play the game? To find out we need to load the value function we have calculated and visualise it.
value_100 = np.zeros((100, equivalent_action_num_state_space.next_index))
count_100 = np.zeros((100, equivalent_action_num_state_space.next_index))
for i in range(100):
value_100[i, :] = np.load('value_table_equiv_num' + str(i) + '.npy')
count_100[i, :] = np.load('count_table_equiv_num' + str(i) + '.npy')
total_value = np.multiply(value_100, count_100)
count_summed = np.sum(count_100, axis=0)
value_summed = np.sum(total_value, axis=0)
valid = count_summed != 0
mean_value_equiv_num = np.zeros(count_summed.shape)
mean_value_equiv_num[valid] = np.divide(value_summed[valid],
count_summed[valid])
There is no obvious way to visualise the value function as it is quite complex. One strategy is to see how it changes as we vary each parameter. In the functions below we specify a parameter to consider the effect of and we plot a line for each set of states where the only difference is the value of the parameter we are considering.
def vary_one_parameter(param_to_vary, other_params):
"""
param_to_vary should be a dict with one element where the key is one of the
arguments which can be passed to SingleCardNumState and the value is a
range of valid values for this parameter
other_params should be a dict with elements like param_to_vary for all other
SingleCardNumState arguments.
We consider the effect of varying param_to_vary in the range passed and we
plot a line for each set of states where the only difference is the value
of the parameter we are considering
"""
assert len(param_to_vary) == 1
plt.figure()
plt.xlabel(next(iter(param_to_vary.keys())))
plt.ylabel('Value')
args_dict_so_far = {}
loop_through_next_parameter(param_to_vary, other_params, args_dict_so_far)
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5), ncol=2)
def loop_through_next_parameter(param_to_vary, other_params, args_dict_so_far):
"""
param_to_vary should be a dict with one element where the key is one of the
arguments which can be passed to SingleCardNumState and the value is a
range of valid values for this parameter
other_params should be a dict with like param_to_vary for other
SingleCardNumState arguments
args_dict_so_far should be a dict of other SingleCardNumState arguments to
single values for them.
Whilst there are still elements in other_params pop one, loop through the
range passed set the value in the args_dict_so_far and recursively call
this function.
When all other params are set vary the param in param_to_vary and plot a
line for it.
"""
if other_params:
current_other_params = copy.deepcopy(other_params)
# Pick an element from other_params and call this function for each
# value it can take
param_name, param_range = current_other_params.popitem()
for param in param_range:
current_args_dict = copy.deepcopy(args_dict_so_far)
current_args_dict[param_name] = param
loop_through_next_parameter(param_to_vary, current_other_params,
current_args_dict)
else:
current_args_dict = copy.deepcopy(args_dict_so_far)
current_values = {}
label_str = ', '.join([k + ' ' + str(v)
for k, v in current_args_dict.items()])
current_param_to_vary = copy.deepcopy(param_to_vary)
param_name, param_range = current_param_to_vary.popitem()
# Let param to vary take each possible value
for param in param_range:
current_args_dict[param_name] = param
if current_args_dict['num_played'] == 0:
current_args_dict['last_card'] = -1
else:
current_args_dict['last_card'] = 0
state = SingleCardNumState(**current_args_dict)
sap = equivalent_action_num_state_space.state_action_pairs
if state in sap:
index = sap[state][0]
current_values[param] = mean_value_equiv_num[index]
if len(current_values) > 1:
plt.plot(np.array([k for k in current_values.keys()]),
np.array([v for v in current_values.values()]),
label=label_str)
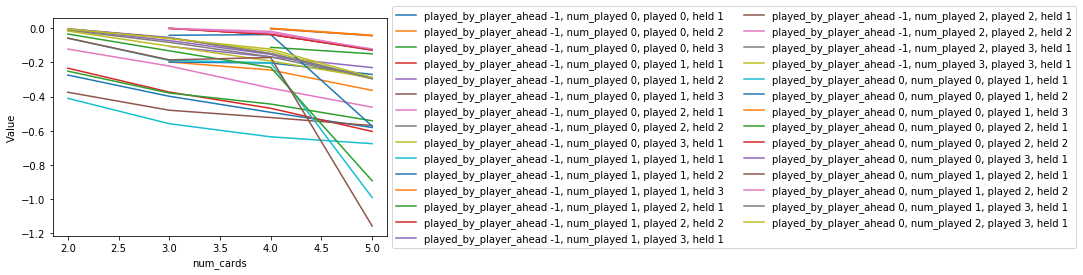
As we increase the number of cards held the value decreases. This is because we hold more cards at the beginning of episodes when we have more time to accumulate negative rewards. Some of the lines look quite different, with the value sharply decreasing as we go from 4 cards held to 5 cards held. These are the states where the card we are considering playing has been played by the player ahead. Since the other players all follow the simple strategy if the player ahead has 2 of the same card type they will choose to play it instead of cards that they only have one of. This means that if it was played by the player ahead when the agent still has 5 cards it is a very poor choice, whereas if it was played by the player ahead when the agent has 4 cards it is usually a good choice since it is uncommon for the player ahead to start with 3 the same.
params = {'held' : range(1, 5), 'played' : range(0, 4),
'num_played' : range(0, 4), 'played_by_player_ahead' : [-1, 0]}
param_to_vary = {'num_cards' : range(2, 6)}
vary_one_parameter(param_to_vary, params)
Unsurprisingly, the more of a card type that we hold the better the value of playing it.
params = {'num_cards' : range(2, 6), 'played' : range(0, 4),
'num_played' : range(0, 4), 'played_by_player_ahead' : [-1, 0]}
param_to_vary = {'held' : range(1, 5)}
vary_one_parameter(param_to_vary, params)

Similarly, when more cards have been played we get a better value for playing the same card. When 3 cards have been played and we hold the other one, there is no chance of getting a negative reward in the next step so the values for these states converge on the expected cumulative reward for the rest of the episode which just depends on the number of cards held.
params = {'num_cards' : range(2, 6), 'held' : range(1, 5),
'num_played' : range(0, 4), 'played_by_player_ahead' : [-1, 0]}
param_to_vary = {'played' : range(0, 4)}
vary_one_parameter(param_to_vary, params)

Considering whether cards have been played immediately before the agent’s turn, we have 2 cases. In some cases the value stays constant, these are the cases where all of the cards of this type are either held by the player or already played, in which case the value is just determined by the number of cards left to play. In other cases the value decreases. This is because if the player ahead plays the same card as us we get a larger negative reward when the previous players have played the same card as us. Of course, this is a reduced version of the full game where there is no benefit to making others lose money. An interesting extension would be to model the full game where we only get a reward once all other players have lost 5 pence. In the full game it may be that the value increases when we play a card that has been played many times before.
params = {'num_cards' : range(2, 6), 'held' : range(1, 5),
'played' : range(0, 4), 'played_by_player_ahead' : [-1, 0]}
param_to_vary = {'num_played' : range(0, 4)}
vary_one_parameter(param_to_vary, params)

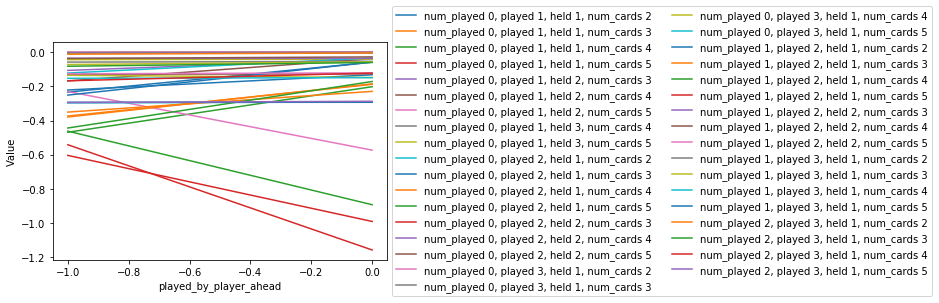
Finally, we have the difference between if the card was played by the player ahead or not. In some cases we are better off if the card was played by the player ahead, these are the cases where we have few cards remaining so the player ahead is likely to have already used any cards that they have duplicates of. In other cases we are worse off if the card was played by the player ahead, in these cases the number of cards held is 5, because the player ahead is likely to be using duplicates early in the episode.
params = {'num_cards' : range(2, 6), 'held' : range(1, 5),
'played' : range(0, 4), 'num_played' : range(0, 4)}
param_to_vary = {'played_by_player_ahead' : [-1, 0]}
vary_one_parameter(param_to_vary, params)
These insights give us some idea about how to value different states. It is still fairly difficult to summarize all of the information gained in a way which is easy to remember so it may be necessary for me to spend some time memorising the 100 different states and their values before I play the game again next Christmas.
